Никто не знает, как построить на плоскости самую маленькую фигуру, способную закрыть все другие фигуры определённой ширины. Но геометрия средней школы позволяет приблизиться к решению этой задачи.
Предположим, что вы изумительно владеете иголкой и ниткой. Ваш друг, зная об этом, написал вам письмо с просьбой о помощи: «Эй, у меня есть джинсы, которые прохудились. Можешь ли ты залатать их для меня?»
«Конечно! Это легко, — отвечаете вы. — А какого размера дырки?»
«Они все разные и неправильных форм, но не шире дюйма. Я заскочу чуть позже, так что готовься!»
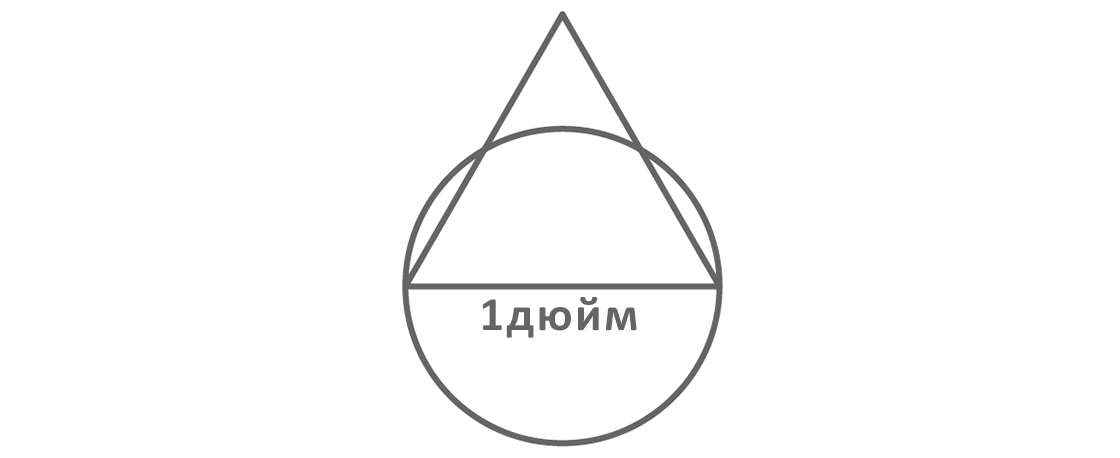
Вы достаёте свой швейный набор и берёте оттуда несколько круглых кусочков ткани, каждый диаметром 1 дюйм. «Это должно подойти», — думаете вы. Но подойдёт ли? Действительно ли круглая заплатка диаметром 1 дюйм способна закрыть любую дырку шириной не более 1 дюйма в любом направлении?
Вы берёте из своего набора кусочек ткани в виде равностороннего треугольника с однодюймовыми сторонами. Между двумя точками в этом треугольнике, отмечаете вы, расстояние не более 1 дюйма, поэтому какая-то из дырок в джинсах вашего друга вполне может иметь такую же форму. Но, наложив на треугольник один из заготовленных вами кругляшей, вы замечаете, что круглая заплатка закрывает лишь две вершины треугольника, а третья остаётся открытой.
Дело в том, что, согласно элементарной геометрии, высота данного треугольника 
Вы можете просто-напросто взять такой большой кругляш, который гарантирует вам успех, но вы не хотите понапрасну тратить драгоценный материал. Поэтому встаёт вопрос: каким должен быть наименьший кусок ткани, способный закрыть дырку шириной не более 1 дюйма? Поискав ответ онлайн, вы узнаете, что математики тоже размышляют над этим вопросом: они более 100 лет ищут универсальную форму минимальной заплаты. Эта идеальная форма всё ещё не найдена, но благодаря недавним исследованиям удалось значительно продвинуться вперёд.
Впервые «проблема универсального покрытия» была поставлена в 1914 году Анри Лебегом (Henri Lebesgue) в его письме коллеге-математику Юлиусу Палу (Julius Pál). Задачу можно формулировать по-разному, но в её основе лежит понятие «области единичного диаметра». Здесь имеется в виду множество точек плоскости, в котором нет двух точек, отстоящих друг от друга более чем на 1 единицу. В нашей задаче о починке штанов это — дыра шириной не более 1 дюйма.
Если одно множество точек может поместиться внутри другого, говорят, что второе множество «покрывает» первое — подобно заплате, закрывающей дырку. «Универсальное покрытие» — это область, которая способна покрыть все формы единичного диаметра, и, чтобы решить проблему универсального покрытия Лебега, требуется получить наименьшую выпуклую область. («Выпуклая», если объяснять нестрого, означает, что у искомого покрытия нет никаких выемок, а «наименьшая» — «с минимальной площадью»).
Вас может удивить, что прошло 100 лет, а эту геометрическую задачу, которая, похоже, является элементарной, решить не сумели. Однако, на самом деле, задача Лебега — отнюдь не простая, и отчасти потому, что трудно точно изобразить искомую форму единичного диаметра. Как нам известно, доказательство теорем о свойствах предмета, который не удаётся чётко представить, может оказаться весьма трудным занятием.
Чтобы покрыть все множества единичного диаметра, нужны «заплаты» подходящих форм. Мы знаем много таких форм, но ни одна из них не является наименьшей. Давайте выясним, почему математикам никак не удаётся скроить «заплату» искомой формы.
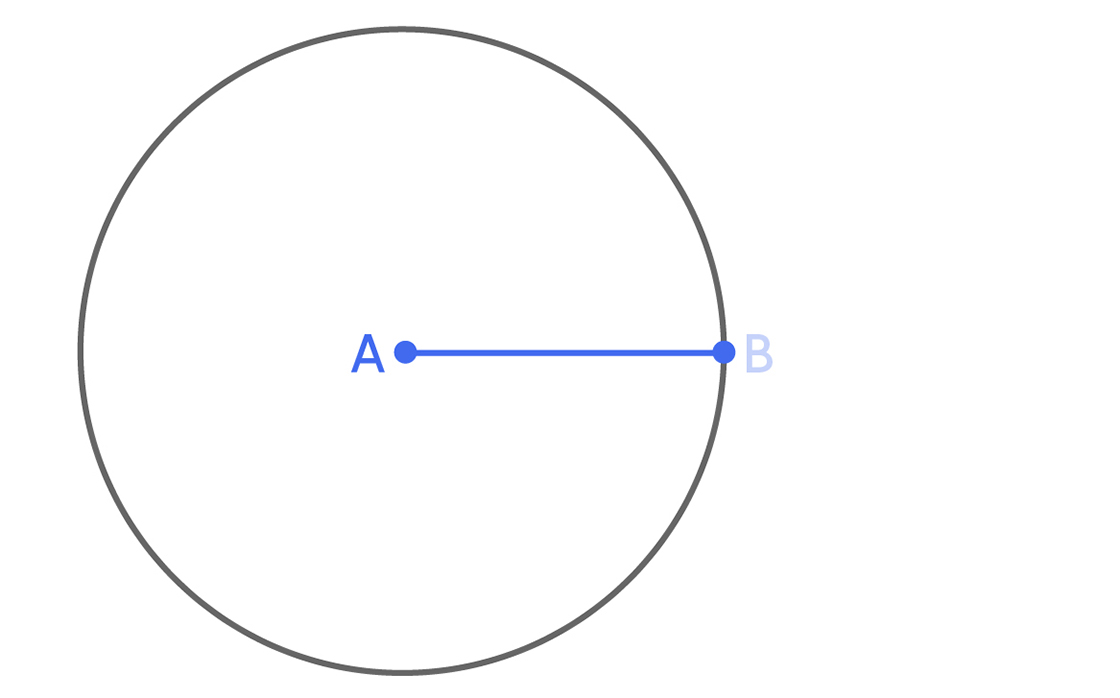
Начнём с области R единичного диаметра. Мы понятия не имеем, как выглядит R; нам всего лишь известно, что, так же как и дыры, которые требуется закрыть этой областью, её ширина не превышает единицы. Однако, поскольку у неё единичный диаметр, предположим, что в неё входят точки A и B, расстояние между которыми составляет 1 единицу.
Теперь предположим, что в R входит и точка C. Где может находиться C? Расстояние от C до А не может быть больше единичного, следовательно, точка С должна находиться в пределах круга единичного радиуса с центром в А. Вы можете построить этот круг с помощью циркуля — с центром в А и окружностью, проходящей через B.
Но расстояние от С до В тоже не может быть больше единичного, поэтому точка С должна находиться в пределах круга единичного радиуса с центром в В. Этот круг тоже можно построить, используя циркуль.
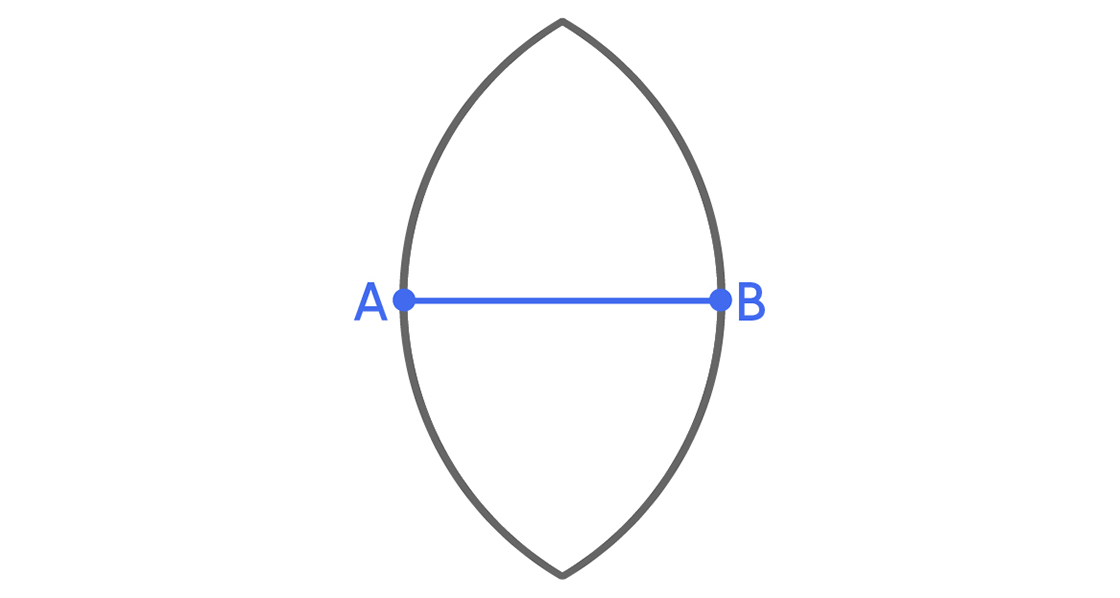
Значит, точка С должна лежать в области пересечения двух этих кругов.
Данное рассуждение относится не только к точке С; оно относится ко всем точкам, входящим в R. Таким образом, любая точка в R должна принадлежать к области пересечения двух построенных нами кругов. Другими словами, эта область может покрыть все возможные множества R единичного диаметра и является универсальным покрытием.
Но это универсальное покрытие не является наименьшим. Давайте попробуем его урезать.
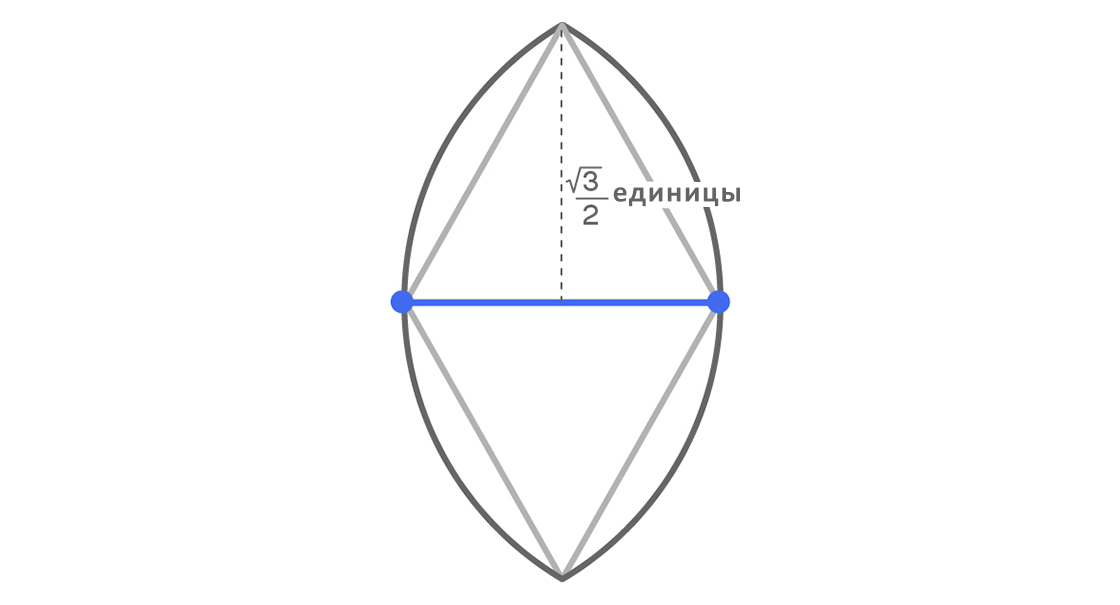
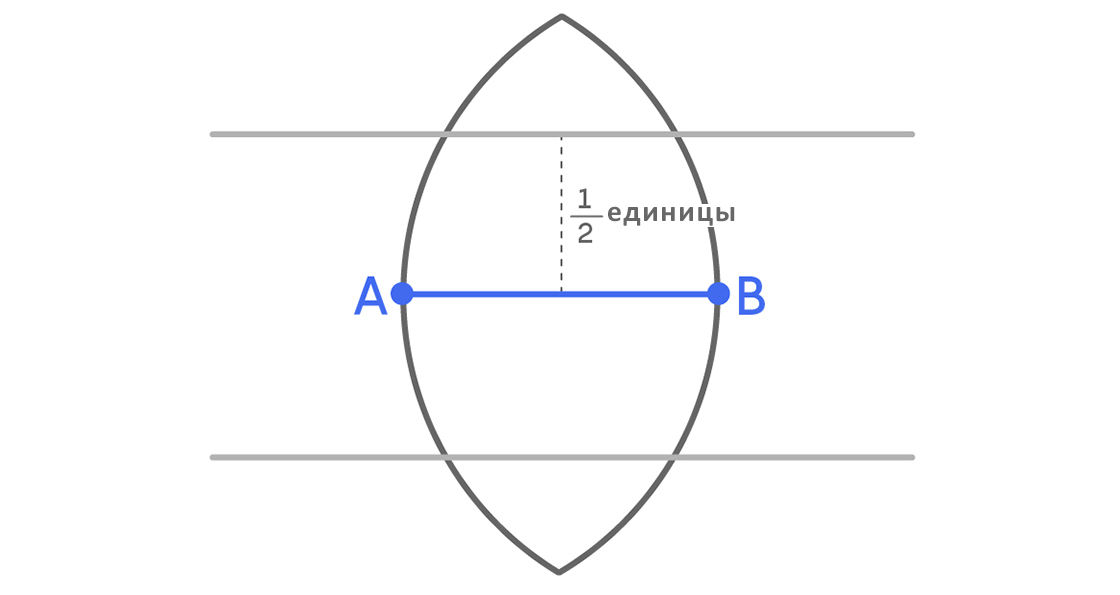
Обратим внимание на то, что точки области пересечения кругов образуют два равносторонних треугольника с A и B, а расстояние от верхней точки (и от нижней) до середины отрезка AB составляет
Так как 
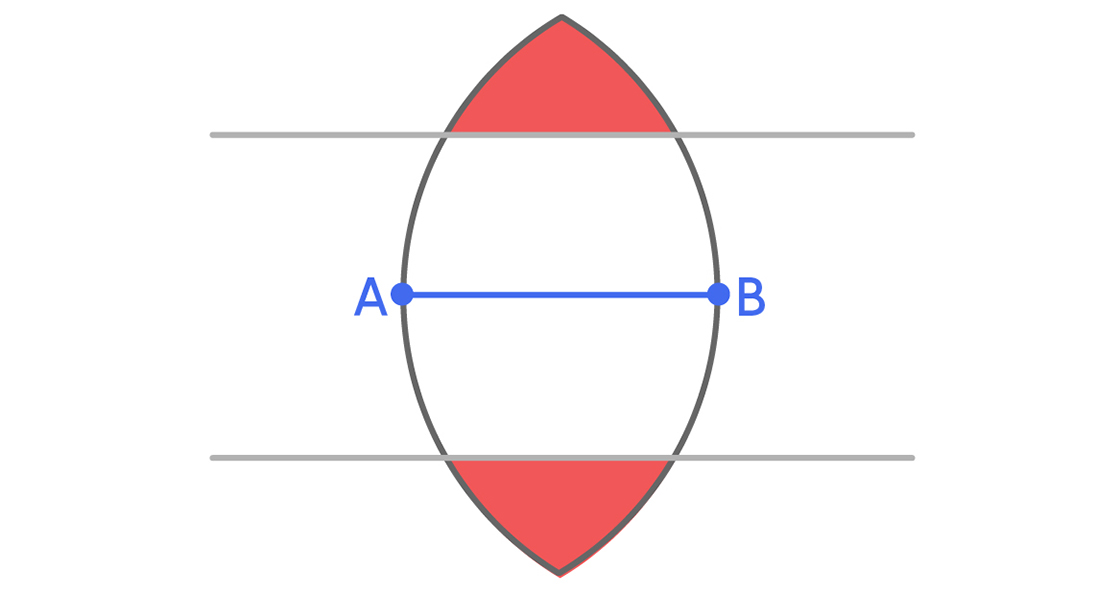
Теперь рассмотрим две области красного цвета, одна из которых находится над верхней параллельной линией, а другая — под нижней.
Поскольку расстояние между двумя параллельными линиями равно единице, множество единичного диаметра не может одновременно находиться в обеих красных областях. Это значит, что для универсального покрытия обе красные области не нужны. Одну мы можем просто-напросто удалить.
Исходно полученное нами покрытие — область пересечения двух кругов — имеет площадь 
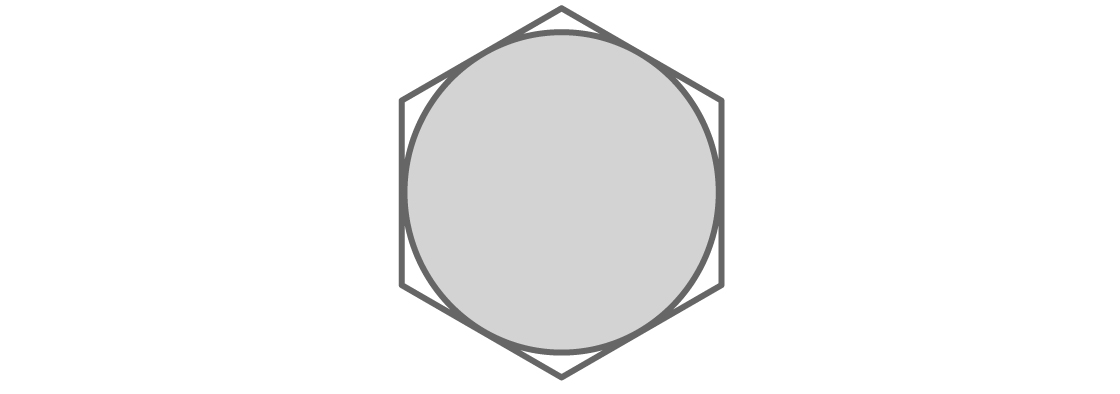
Именно так математики пришли к полученной нами версии наименьшего универсального покрытия. Используя более продвинутые методы, мы можем найти другие простые формы, чтобы потом улучшать их. Например, можно показать, что универсальным покрытием является квадрат со стороной, равной единице. А Пал, решая задачу Лебега, использовал свойства так называемых «кривых постоянной ширины». С помощью этих кривых он показал, что даже если какая-то часть множества единичного диаметра «вылезла» за пределы закрывающего его круга единичного диаметра, оно всегда может быть смещено или повёрнуто так, что его полностью закроет шестиугольник, в который вписан этот круг:
Ниже показано, как шестиугольник Пала закрывает фигуры единичного диаметра трёх разных форм. Форма в середине — это треугольник Рёло (Reuleaux), кривая постоянной ширины, тесно связанная с рассмотренными нами выше примерами покрытий. (Чтобы построить треугольник Рёло, используя наши примеры, нужно из верхней точки области пересечения двух кругов провести дугу единичного радиуса от A до B).
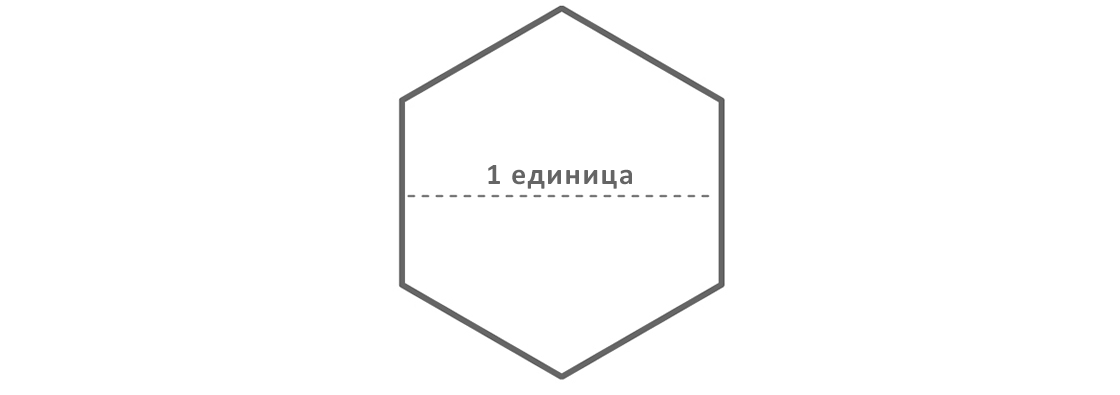
Данный шестиугольник имеет площадь 
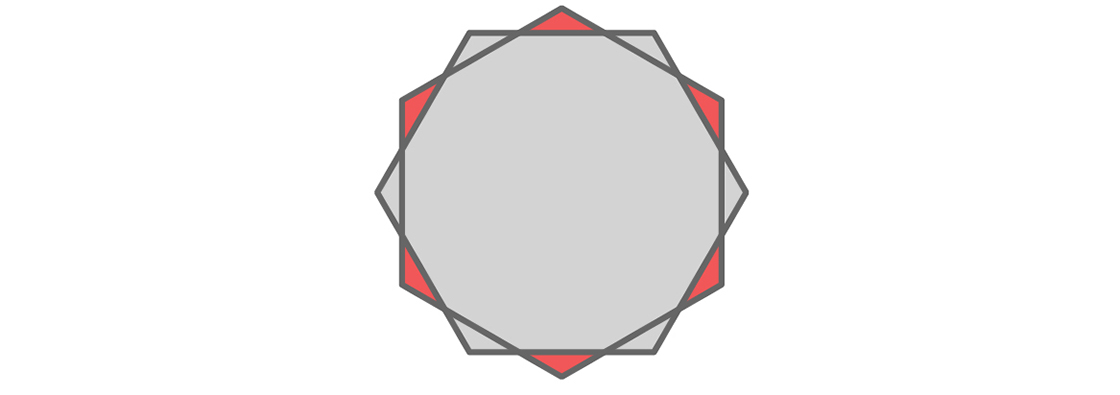
Начнём с двух копий шестиугольника Пала, сложенных вместе,
и повернём одну из них на 30 градусов вокруг их общего центра.
Благодаря этому появляется масса любопытных вещей — например, область пересечения двух шестиугольников представляет собой додекагон, — но нас больше всего интересуют шесть маленьких красных треугольников, изображённых ниже.
Каждый красный треугольник находится внутри шестиугольника, который мы не вращали, и снаружи повёрнутого шестиугольника. Поскольку расстояние между двумя любыми противоположными сторонами обоих шестиугольников составляет единицу, расстояние между точками внутри двух противоположных красных треугольников должно быть больше единицы. Как и в нашем рассуждении, приведённом выше, универсальному покрытию не нужны оба треугольника из каждой пары противоположных друг другу треугольников, поскольку множество единичного диаметра не может находиться одновременно в обоих. Следовательно, у нас есть возможность удалить некоторые треугольники, и, по-видимому, их будет три (по одному из каждой пары). Но, к сожалению, удалив три красных треугольника, мы лишим наше покрытие способности закрывать любые множества единичного диаметра. Давайте выясним почему.
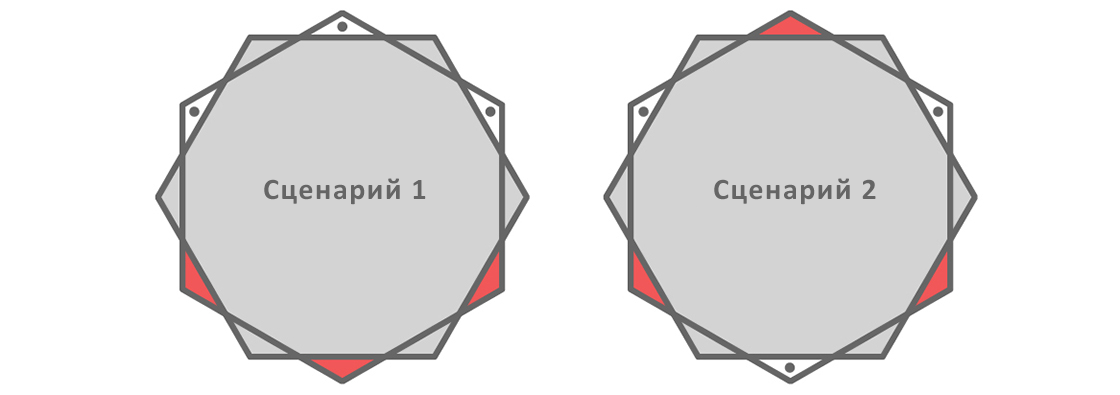
Чтобы при вращении шестиугольник не претерпел никаких изменений, его можно повернуть на 60 градусов или по одной из осей симметрии, поэтому, в действительности, есть только два способа выбрать один красный треугольник из каждой пары противоположных друг другу треугольников: можно взять три следующих друг за другом треугольника или каждый второй из шести треугольников. Это показано ниже. Точки указывают на те треугольники, которые может занимать множество единичного диаметра.
Если множество, которое следует покрыть, занимает три последовательных треугольника, как показано слева, его не сможет закрыть покрытие той формы, которая получается при удалении каждого второго из шести треугольников, как показано справа. А если это множество занимает каждый второй из шести треугольников, его не сможет закрыть покрытие, имеющее форму, получаемую при удалении трёх следующих друг за другом треугольников. Удаление любого множества, состоящего из трёх треугольников, оставляет возможность того, что некое множество единичного диаметра не будет закрытым. Следовательно, мы не можем удалить три красных треугольника.
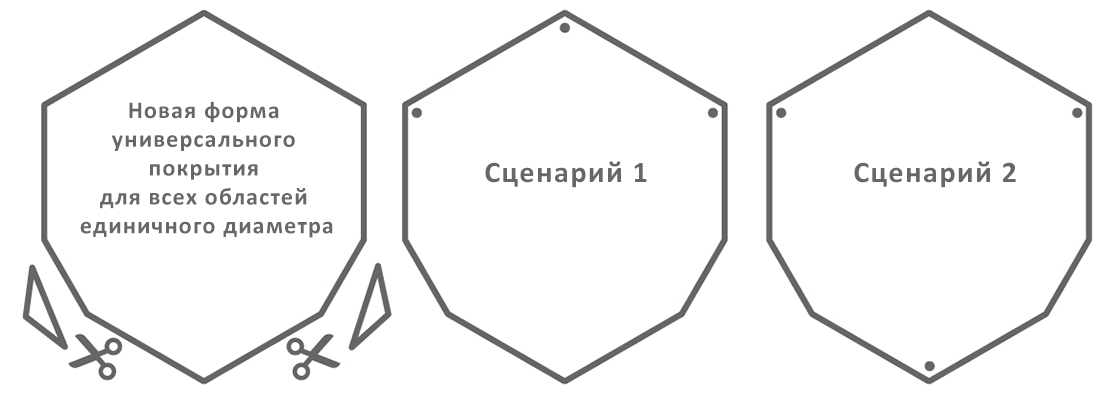
Но мы можем удалить два. Два проблемных множества, описанных выше, всё же могут быть закрыты, если мы удалим два красных треугольника, которые не являются ни соседними, ни противоположными. Именно так и поступил Пал.
Чтобы получить новую форму, полностью закрывающую любую область единичного диаметра, он отрезал от своего шестиугольника два треугольника. У этого нового универсального покрытия площадь немного меньше, чем у шестиугольника: 
На этом отрезание лишних кусков не закончилось. Куски меньшего размера успешно удалили математики Роланд Шпраг (Roland Sprague) и Х. Хансен (H.C. Hansen) — в 1936 и 1992 годах соответственно. А всего несколько лет назад математик-любитель Филип Гиббс (Philip Gibbs) предложил отрезать несколько новых кусочков. Его вдохновила на это публикация математика-блогера Джона Баэза (John Baez). Совместно с Баэзом и ещё одним математиком Гиббс обобщил методы Шпрага и Хансена, чтобы ещё больше урезать покрытие. В результате был установлен новый мировой рекорд в деле создания наименьшего выпуклого покрытия для множеств единичного диаметра. Это достижение быстро улучшил сам же Гиббс, дополнительно удалив лишние области.
Прекрасно, что отрезание лишних кусочков от шестиугольника Пала продолжается, да только эти кусочки стали крохотными. Немец Шпраг уменьшил площадь покрытия приблизительно на 0,001 квадратной единицы, а датчанин Хансен — всего лишь на 0,00000000004 квадратной единицы. Гиббс и те, кто с ним работал, сократили покрытие Хансена примерно на 0,00002 квадратной единицы, что по сравнению с рекордом датчанина выглядит огромным достижением.
До какого наименьшего результата можно дойти? В 2005 году Питер Брасс (Peter Brass) и Мербод Шарифи (Mehrbod Sharifi) доказали, что универсальное покрытие не может быть меньше 0,832 квадратной единицы, поэтому нам известно, что нынешний рекорд нельзя улучшить намного. Однако, если вам удастся придумать новый метод или новую отправную точку, вы можете приблизить к нам минимальное универсальное покрытие и отрезать для себя кусочек истории математики. Только помните, что самое сложное — представить бесконечно много вариантов формы, доступных для множества единичного диаметра. И убедиться, что, создав своё покрытие, вы все их учли.
